O Grau
Definimos como 1 grau o arco equivalente a  a circunferência, isto é, em uma circunferência cabem 360 º.
a circunferência, isto é, em uma circunferência cabem 360 º.
Exemplos:
Dividindo a circunferência em 4, 6 e 8 partes congruentes, temos:



O grau comporta ainda os submúltiplos, minuto(,) e segundo(,,), de forma que:
1º =60' e 1'`=60,,
O Radiano
Definimos 1 radiano como o arco cujo comprimento é igual ao raio da circunferência onde tal arco foi determinado.
A partir da figura, imagine que o arcos AB foi retificado. O Segmento AB obtido, tendo comprimento igual ao raio da circunferência, indica que a medida do arco, em radianos, equivale ao número de vezes que o comprimento do raio cabe nesse arco, ou seja, sendo 1 e R os comprimentos do arco e do raio da circunferência, respectivamente, temos:
a=1/R
Lembramos que o comprimento de uma circunferência de raio R é dado por 2pR. Utilizando a relação apresentada acima, para calcularmos em radianos a medida a de um arco de uma volta, fazemos:
alfa=2pR/R = 2prad
Exemplos:
Conceituando o Ciclo Trigonométrico
As razões trigonométricas, aplicadas a arcos de uma circunferência, mantêm as mesmas propriedades que demonstramos ser válidas quando utilizadas com ângulos agudos.
Inicialmente, deveremos definir uma circunferência, em especial, sobre a qual interpretaremos as nossas já conhecidas razões trigonométricas.
Tal circunferência recebe o nome de circunferência trigonométrica ou ciclo trigonométrico.
Imaginemos, primeiramente, um sistema de coordenadas cartesianas, como indicado na figura 1.

(figura 1)
Nos eixos r e s, perpendiculares entre si, cada ponto corresponde a um número real e vice-versa: cada número real tem um ponto associado em cada uma das retas. À interseção dos eixos faremos corresponder o número zero, tanto para o eixo r, das abscissas, como para o eixo s, das ordenadas, constituindo o que chamamos de origem dos eixos coordenados.
Assim, qualquer ponto do plano determinado pode ser representado por um par de números reais, a que chamamos de par ordenado. O ponto P, na figura, terá então as coordenadas (a, b), sendo a a abscissa de P e b a sua ordenada.
Na figura 2, fazemos surgir o ciclo trigonométrico, com centro na origem dos eixos e raio unitário.

(figura 2)
Como consequência, os pontos de interseção da circunferência com o par de eixos, indicados na figura por A, B, C e D, terão coordenadas dadas respectivamente por (1, 0), (0, 1), (_ 1, 0) e (0, _ 1).
Esses pontos dividem o ciclo trigonométrico em quatro arcos congruentes, aos quais damos o nome de quadrantes, numerados a partir de A no sentido anti-horário.
Por convenção, A, B, C e D são apenas limitadores dos quadrantes, não pertencendo a nenhum deles. Por exemplo, D é ponto que separa 3º do 4º quadrantes, mas não lhes pertence.
Números Reais no Ciclo Trigonométrico
Vamos associar a cada número real x um ponto do ciclo trigonométrico, de tal forma que:
_ o ponto A esteja associado ao número x = 0;
_ um número real x seja associado a um ponto P, tal que o comprimento do arco seja igual a | x |;
_ se x > 0, o arco será determinado, sobre o ciclo, no sentido anti-horário; se x < 0, o arco será
definido no sentido horário, como indicamos na figura 3.

(figura 3)
O ponto P, determinado de acordo com o que apresentamos acima, associado a um número real x, é denominado de imagem de x no ciclo trigonométrico.
Lembremos que o comprimento da circunferência trigonométrica pode ser calculado por C = 2R, sendo R o seu raio.
Como ele tem por medida uma unidade, o comprimento do ciclo trigonométrico será igual, portanto, a 2 unidades. Como decorrência, temos que:
_ um arco de uma volta (ou de medida 2 rad) terá comprimento 2 unidades;
_ um arco de comprimento |x|, no ciclo trigonométrico, terá medida |x| rad.
Assim, a medida de um arco , sobre o ciclo trigonométrico, é igual ao módulo do número real x do qual P é a imagem.
Círculo Trigonométrico é um círculo de centro na origem do referencial e raio igual à unidade, ao qual se encontra associado um referencial ortonormado xOy.
 Consideremos sobre o círculo trigonométrico de centro O, os pontos A e B escolhidos como a figura indica.
Consideremos sobre o círculo trigonométrico de centro O, os pontos A e B escolhidos como a figura indica.
 Se aos pontos A e B fizermos corresponder as semi-rectas OA e OB, o par (OA,OB) define um ângulo.
Se aos pontos A e B fizermos corresponder as semi-rectas OA e OB, o par (OA,OB) define um ângulo.  O ponto O é o vértice do ângulo e as semi-rectas OA e OB são, respectivamente, o lado origem e o lado extremidade.
O ponto O é o vértice do ângulo e as semi-rectas OA e OB são, respectivamente, o lado origem e o lado extremidade.  Há dois sentidos de percurso num círculo:
Há dois sentidos de percurso num círculo: Ângulo positivo (ou directo) é o ângulo gerado no sentido contrário ao dos ponteiros do relógio.
Ângulo negativo (ou indirecto) é o ângulo gerado no sentido dos ponteiros do relógio.
 A um ângulo pode associar-se uma amplitude em sentidos chamando-se então ângulo orientado.
A um ângulo pode associar-se uma amplitude em sentidos chamando-se então ângulo orientado.
LINHAS TRIGONOMÉTRICAS
 P é o ponto de intersecção do lado extremidade do ângulo com o arco que limita o círculo trigonométrico.
P é o ponto de intersecção do lado extremidade do ângulo com o arco que limita o círculo trigonométrico. O seno de a é a ordenada do ponto P.
O co-seno de a é a abcissa do ponto P.
C é o ponto de intersecção do lado extremidade do ângulo com o eixo das tangentes.
A tangente de a é a ordenada do ponto C.
D é o ponto de intersecção do lado extremidade do ângulo com o eixo das co-tangentes.
A co-tangente de a é a abcissa do ponto C.
Enquadramento de seno e do co-seno
 O sinal de uma razão trigonométrica depende exclusivamente do sinal das coordenadas do ponto associado ao círculo trigonométrico.
O sinal de uma razão trigonométrica depende exclusivamente do sinal das coordenadas do ponto associado ao círculo trigonométrico. Para todo o a,
Para todo o a,
Redução ao 1º quadrante
 Observando atentamente no círculo trigonométrico cada uma das situações em causa, é possível concluirmos algumas relações importantes entre as relações trigonométricas de certos ângulos.
Observando atentamente no círculo trigonométrico cada uma das situações em causa, é possível concluirmos algumas relações importantes entre as relações trigonométricas de certos ângulos. Ângulos do 1ª Quadrante
Ângulos Complementares: a e 90°- a
 Os pontos P e Q do círculo trigonométrico, respectivamente associados a a e a 90-a, são simétricos em relação à recta de equação y = x.
Os pontos P e Q do círculo trigonométrico, respectivamente associados a a e a 90-a, são simétricos em relação à recta de equação y = x. Daí resulta que a abcissa de um é a ordenada do outro e reciprocamente, isto é,
Ângulos do 2º Quadrante
Ângulos que diferem de 90°: a e 90° + a
 A abcissa de Q é simétrica da ordenada de P, e a ordenada de Q é igual à abcissa de P, isto é,
A abcissa de Q é simétrica da ordenada de P, e a ordenada de Q é igual à abcissa de P, isto é, Ângulos Suplementares: a e 180° - a
 Os pontos P e Q do círculo trigonométrico, respectivamente associados a a e 180°- a, são simétricos em relação ao eixo das ordenadas. Daí resulta que as ordenadas de P e Q são iguais e as suas abcissas são simétricas, isto é,
Os pontos P e Q do círculo trigonométrico, respectivamente associados a a e 180°- a, são simétricos em relação ao eixo das ordenadas. Daí resulta que as ordenadas de P e Q são iguais e as suas abcissas são simétricas, isto é, Ângulos do 3º Quadrante
Ângulos que diferem de 180º: a e 180° + a
 Os pontos P e Q do círculo trigonométrico, respectivamente associados a a e a 180° + a, são simétricos em relação a O.
Daí resulta que as suas ordenadas e as suas abcissas são simétricas, isto é,
Ângulos que somados valem 270º: a e 270º - a
Ângulos do 4º Quadrante
Ângulos que diferem de 270º: a e 270º + a
Os pontos P e Q do círculo trigonométrico, respectivamente associados a a e a 180° + a, são simétricos em relação a O.
Daí resulta que as suas ordenadas e as suas abcissas são simétricas, isto é,
Ângulos que somados valem 270º: a e 270º - a
Ângulos do 4º Quadrante
Ângulos que diferem de 270º: a e 270º + a
Ângulos Simétricos: a e -a
 Os pontos P e Q do círculo trigonométrico, respectivamente associados a e -a, são simétricos em relação ao eixo das abcissas.
Daí resulta que as abcissas de P e Q são iguais e as suas ordenadas são simétricas, isto é,
OBS.: As relações que acabamos de estudar são válidas qualquer que seja a amplitude a do ângulo (em graus ou radianos).
Valores de algumas razões trigonométricas:
Os pontos P e Q do círculo trigonométrico, respectivamente associados a e -a, são simétricos em relação ao eixo das abcissas.
Daí resulta que as abcissas de P e Q são iguais e as suas ordenadas são simétricas, isto é,
OBS.: As relações que acabamos de estudar são válidas qualquer que seja a amplitude a do ângulo (em graus ou radianos).
Valores de algumas razões trigonométricas:
| 0° | 30° | 45° | 60° | 90° |
sen | 0 | | | | 1 |
cos | 1 | | | | 0 |
tg | 0 | | 1 | | ¥ |
cotg | ¥ | | 1 | | 0 |
|
Fórmulas Trigonométricas
Fórmula Fundamental
 Fórmulas Secundárias
Fórmulas Secundárias




 Fórmulas de Adição
Fórmulas de Adição





 Fórmulas de Duplicação
Fórmulas de Duplicação





 Fórmulas de Bissecção
Fórmulas de Bissecção


 Fórmulas de Transformação
Fórmulas de Transformação





Obs: Os exercícios serão realizados em sala.




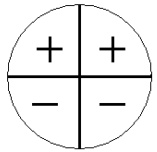
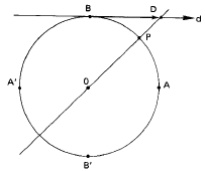
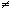 kπ, considerando a reta s tangente ao circulo trigonométrico no ponto P que intercepta o eixo do seno no ponto C, definimos por cossecante o módulo do segmento que vai do centro da circunferência trigonométrica até o ponto C.
kπ, considerando a reta s tangente ao circulo trigonométrico no ponto P que intercepta o eixo do seno no ponto C, definimos por cossecante o módulo do segmento que vai do centro da circunferência trigonométrica até o ponto C.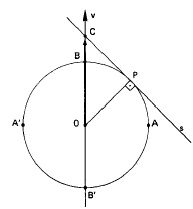
 a circunferência, isto é, em uma circunferência cabem 360 º.
a circunferência, isto é, em uma circunferência cabem 360 º.




























